Appealing Choices
Weapon selection is about choosing the most appropriate weapon for the job. This much is obvious, but it raises two questions: How do you define "appropriate," and how do you pick the best weapon? Let's elaborate on these issues in turn, looking at the concepts at the base of the problem.
A Theory for Weapon Evaluation
First, we need to understand how the properties of the environment are taken into account, and then discuss the essence of weapon evaluation.
Features and Criteria
As discussed in the preceding chapter, many features of the environment, enemy player, or spatial configuration can be taken into account. These features can be modeled as a set of features [f1,f2,...fn], either symbols or numeric values (that is, heterogeneous).
Each person may have different goals and motivations, so these features will be taken into account differently according to a set of criteria [c1,c2,...cm]. For example, these may represent the desire to limit self-injury, inflict maximum damage, or alert the enemy. For those players with better skills, criteria can correspond to other measurable benefits, such as minimizing fight time and judicious use of ammo.
In games, players may increasingly select weapons for entertainment purposes, or to encourage diversity in the gameplay. As such, the set criteria may include different goals in practice, but these can be applied in the same fashion—theoretically speaking.
Weapon Fitness
Whether a complex system of desires and motivations drives the selection process, or a unique goal instead, the problem can be simplified to a fundamental level. All the details about the situation, the state of the player, or even the properties of the weapon can be abstracted out.
Only a single number is needed to indicate the benefit of weapon; in the current situation, how good is this weapon? This is a single continuous value, which we'll call the fitness of a weapon.
The process of determining the applicability of a weapon can be seen as a fitness function. The idea is that an unknown function encodes all the decision criteria or features that are taken into account in the decision. This function f can be applied to each weapon considered as a choice, resulting in a scalar value k (not necessarily limited to a discrete range):

In the case of weapon selection, the scalar value k would indicate how "fit" the weapon w W is (on any scale). For a simple game, the set of all weapons may be defined as W = {rocket launcher, chaingun, blaster}. The fitness function can be can be modeled formally, expressing the mapping from the set of weapons W to the set of real numbers R: W is (on any scale). For a simple game, the set of all weapons may be defined as W = {rocket launcher, chaingun, blaster}. The fitness function can be can be modeled formally, expressing the mapping from the set of weapons W to the set of real numbers R:

By understanding the features and criteria, the problem can be modeled in more detail. Specifically, instead of seeing f as a mystery function, we can express it in terms of the features and criteria:

This equation describes a function g, which can map the features and criteria onto another function (denoted W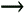 R). For future reference, this is the notation used in functional programming, a type of language that allows functions to return functions. Essentially in this case, it's possible to build a fitness function for evaluating weapons from sets of criteria and features. R). For future reference, this is the notation used in functional programming, a type of language that allows functions to return functions. Essentially in this case, it's possible to build a fitness function for evaluating weapons from sets of criteria and features.
These criteria can be taken into account in different ways, some more intricate than others. For example, a linear model is probably the simplest: 65 percent f1 and 35 percent c2. This corresponds to weighted contributions in the final fitness value. Nonlinear functions would be more appropriate, allowing criteria to rank the importance of features.
Selection Methodology
The concept of fitness to allow weapons to be selected is this: If someone makes a decision to pick a weapon w, and claims it's his best choice, the weapon will certainly maximize some unknown fitness function f (that is, w has the largest value of k). All weapons x ( x) except w (x x) except w (x W – {w}) would presumably have lower fitness: W – {w}) would presumably have lower fitness:

So, a considered decision would go through all the choices and compare their fitness—explicitly ranking them. By discarding the worst option at each comparison, the best choice will remain in the end. This is an expensive procedure of complexity O(n); the AI needs n comparisons to guarantee it has the best choice.
When humans make a choice, they go through a similar process, although often not consciously. It's rarely important, and the process is rushed for practical reasons (for instance, picking vegetables at the store).
It seems obvious that the essence of the decision lies in the unknown fitness function, which evaluates the benefit of each alternative. Some understanding of the animat's motives is needed to design the AI; therefore, a fitness function can be implemented, which is used to evaluate a decision. This is the tricky part; the rest is just methodology.
|  Free JavaScript Editor
Ajax Editor
Free JavaScript Editor
Ajax Editor
 Ajax Editor
JavaScript Editor
Ajax Editor
JavaScript Editor