12.3. Lighting with Spherical Harmonics

In 2001, Ravi Ramamoorthi and Pat Hanrahan presented a method that uses spherical harmonics for computing the diffuse lighting term. This method reproduces accurate diffuse reflection, based on the content of a light probe image, without accessing the light probe image at runtime. The light probe image is preprocessed to produce coefficients that are used in a mathematical representation of the image at runtime. The mathematics behind this approach is beyond the scope of this book (see the references at the end of this chapter if you want all the details). Instead, we lay the necessary groundwork for this shader by describing the underlying mathematics in an intuitive fashion. The result is remarkably simple, accurate, and realistic, and it can easily be codified in an OpenGL shader. This technique has already been used successfully to provide real-time illumination for games and has applications in computer vision and other areas as well.

Spherical harmonics provides a frequency space representation of an image over a sphere. It is analogous to the Fourier transform on the line or circle. This representation of the image is continuous and rotationally invariant. Using this representation for a light probe image, Ramamoorthi and Hanrahan showed that you could accurately reproduce the diffuse reflection from a surface with just nine spherical harmonic basis functions. These nine spherical harmonics are obtained with constant, linear, and quadratic polynomials of the normalized surface normal.

Intuitively, we can see that it is plausible to accurately simulate the diffuse reflection with a small number of basis functions in frequency space since diffuse reflection varies slowly across a surface. With just nine terms used, the average error over all surface orientations is less than 3% for any physical input lighting distribution. With Debevec's light probe images, the average error was shown to be less than 1% and the maximum error for any pixel was less than 5%.

Each spherical harmonic basis function has a coefficient that depends on the light probe image being used. The coefficients are different for each color channel, so you can think of each coefficient as an RGB value. A preprocessing step is required to compute the nine RGB coefficients for the light probe image to be used. Ramamoorthi makes the code for this preprocessing step available for free on his Web site. I used this program to compute the coefficients for all the light probe images in Debevec's light probe gallery as well as the Old Town Square light probe image and summarized the results in Table 12.1.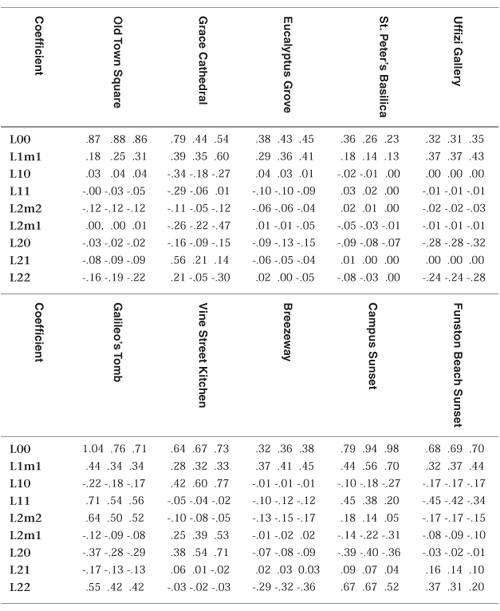

The equation for diffuse reflection using spherical harmonics is

Diffuse = c₁ L₂₂ (x² - y²) + c₃ L₂₀ z² + c₄ L₂₀ - c₅ L₂₀ + 2c₁ (L_{2 - 2} xy + L₂₁ xz + L_{2 - 1} yz) + 2c₂ (L₁₁ x + L_{1 - 1} y + L₁₀ z

The constants c1c5 result from the derivation of this formula and are shown in the vertex shader code in Listing 12.4. The L coefficients are the nine basis function coefficients computed for a specific light probe image in the preprocessing phase. The x, y, and z values are the coordinates of the normalized surface normal at the point that is to be shaded. Unlike low dynamic range images (e.g., 8 bits per color component) that have an implicit minimum value of 0 and an implicit maximum value of 255, high dynamic range images represented with a floating-point value for each color component don't contain well-defined minimum and maximum values. The minimum and maximum values for two HDR images may be quite different from each other, unless the same calibration or creation process was used to create both images. It is even possible to have an HDR image that contains negative values. For this reason, the vertex shader contains an overall scaling factor to make the final effect look right.

The vertex shader that encodes the formula for the nine spherical harmonic basis functions is actually quite simple. When the compiler gets hold of it, it becomes simpler still. An optimizing compiler typically reduces all the operations involving constants. The resulting code is quite efficient because it contains a relatively small number of addition and multiplication operations that involve the components of the surface normal.

Listing 12.4. Vertex shader for spherical harmonics lighting

varying vec3 DiffuseColor; uniform float ScaleFactor; const float C1 = 0.429043; const float C2 = 0.511664; const float C3 = 0.743125; const float C4 = 0.886227; const float C5 = 0.247708; // Constants for Old Town Square lighting const vec3 L00 = vec3( 0.871297, 0.875222, 0.864470); const vec3 L1m1 = vec3( 0.175058, 0.245335, 0.312891); const vec3 L10 = vec3( 0.034675, 0.036107, 0.037362); const vec3 L11 = vec3(-0.004629, -0.029448, -0.048028); const vec3 L2m2 = vec3(-0.120535, -0.121160, -0.117507); const vec3 L2m1 = vec3( 0.003242, 0.003624, 0.007511); const vec3 L20 = vec3(-0.028667, -0.024926, -0.020998); const vec3 L21 = vec3(-0.077539, -0.086325, -0.091591); const vec3 L22 = vec3(-0.161784, -0.191783, -0.219152); void main() { vec3 tnorm = normalize(gl_NormalMatrix * gl_Normal); DiffuseColor = C1 * L22 * (tnorm.x * tnorm.x - tnorm.y * tnorm.y) + C3 * L20 * tnorm.z * tnorm.z + C4 * L00 - C5 * L20 + 2.0 * C1 * L2m2 * tnorm.x * tnorm.y + 2.0 * C1 * L21 * tnorm.x * tnorm.z + 2.0 * C1 * L2m1 * tnorm.y * tnorm.z + 2.0 * C2 * L11 * tnorm.x + 2.0 * C2 * L1m1 * tnorm.y + 2.0 * C2 * L10 * tnorm.z; DiffuseColor *= ScaleFactor; gl_Position = ftransform(); }

Listing 12.5. Fragment shader for spherical harmonics lighting

varying vec3 DiffuseColor; void main() { gl_FragColor = vec4(DiffuseColor, 1.0); }

Once again, our fragment shader has very little work to do. Because the diffuse reflection typically changes slowly, for scenes without large polygons we can reasonably compute it in the vertex shader and interpolate it during rasterization. As with hemispherical lighting, we can add procedurally defined point, directional, or spotlights on top of the spherical harmonics lighting to provide more illumination to important parts of the scene. Results of the spherical harmonics shader are shown in Color Plate 19. Compare Color Plate 19A with the Old Town Square environment map in Color Plate 9. Note that the top of the dog's head has a bluish cast, while there is a brownish cast on his chin and chest. Coefficients for some of Paul Debevec's light probe images provide even greater color variations. We could make the diffuse lighting from the spherical harmonics computation more subtle by blending it with the object's base color.

The trade-offs in using image-based lighting versus procedurally defined lights are similar to the trade-offs between using stored textures versus procedural textures, as discussed in Chapter 11. Image-based lighting techniques can capture and recreate complex lighting environments relatively easily. It would be exceedingly difficult to simulate such an environment with a large number of procedural light sources. On the other hand, procedurally defined light sources do not use up texture memory and can easily be modified and animated.